Back Focus Test Chart (36 cycles with corner stars)
The TE220 is designed for adjustment of camera lenses and checking back focal distance. It consists of a large Siemens star in the center an four smaller ones positioned in the corners of the test chart.
| Type | selectable |
| Format | selectable |
| Aspect ratio | 4:3 |

Chart sizes
The test charts are available in the sizes listed below. Please note that some charts cannot be manufactured in all sizes due to technical reasons. Please do not hesitate to ask for additional information.
During production, specific regions of test charts are measured to qualify the production process or to create individual reference data accompanying a test chart additionally. Measured regions can be color or gray tones.
The measurement devices are calibrated regularly and proven before use. You can find further information in our reference data accuracy sheet.
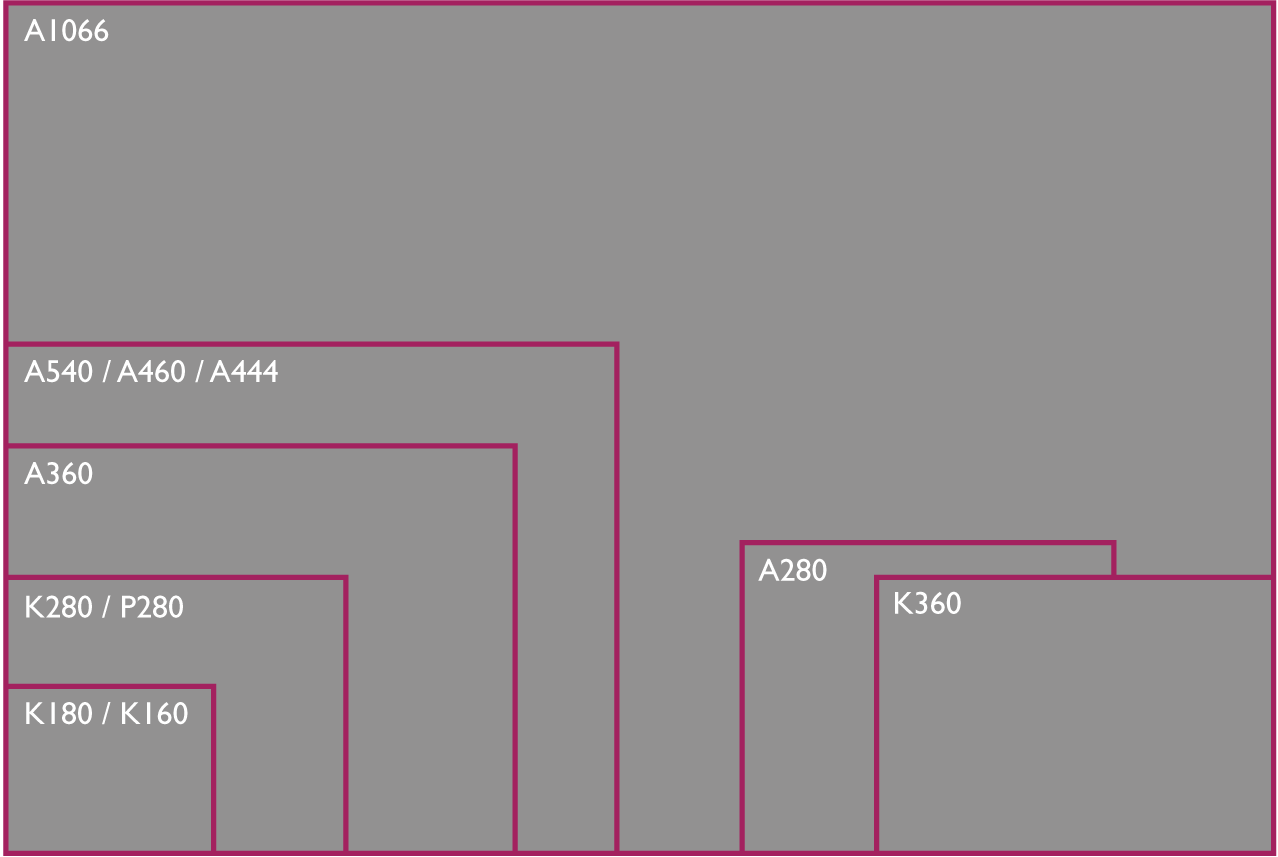
Reflective
| Picture size w x h [mm] | Chart size w x h x d [mm] (+/- 2 mm)* | ||
|---|---|---|---|
| 4:3 | 16:9 | ||
| A1066 | 800 x 600 | - | 1245 x 835 x 3.2 |
| A1066 (TE42*) | 900 x 675 | - | 1245 x 835 x 3.2 |
| A1066 | - | 1066 x 600 | 1400 x 835 x 3.2 |
| A1066 (TE42*) | - | 1200 x 675 | 1400 x 835 x 3.2 |
| A540 | 540 x 405 | 540 x 303.75 | 600 x 500 x 3.2 |
| A460 | 460 x 345 | 460 x 258.75 | 600 x 500 x 3.2 |
| A444 | - | 444.4 x 250 | 600 x 500 x 3.2 |
| A360 | 360 x 270 | 360 x 202.5 | 500 x 400 x 3.2 |
| K360 | - | 360 x 202.5 | 390 x 271 x 2.1 |
| A280 | 280 x 210 | 280 x 157.5 | 365 x 305 x 3.2 |
| K280 | 280 x 210 | 280 x 157.5 | 334 x 271 x 2.1 |
| P280 | May vary in size with the chart layout | 334 x 271 x 2.1 | |
| K180 | - | 180 x 101 | 204 x 164 x 2.1 |
| K160 | 160 x 120 | - | 204 x 164 x 2.1 |
A charts (size 280/360/460) are mounted on aluminium plates.
A charts (size 1066) are mounted on aluminum composite panels (aluminum dibond).
K charts mounted on black polystyrene plates are only available in combination with the test chart folders
P charts are mounted on black polystyrene plates.
*Sizes are for all variations of the TE42 chart series, including TE42 V2, TE42-LL, TE42-LL Timing
Transparent
| Picture size w x h [mm] | Chart size w x h x d [mm] (+/- 2 mm)* | ||
|---|---|---|---|
| 4:3 | 16:9 | ||
| D280 | 280 x 210 | 280 x 157.5 | 360 x 280 x 4.6 |
| D240 | 240 x 180 | 240 x 135 | 320 x 290 x 4.6 |
| D240S | 240 x 180 | 240 x 135 | 360 x 280 x 4.6 |
| D205 | 205 x 153 | 205 x 115.3 | 253 x 202 x 3.5 |
| D120 | 120 x 90 | 120 x 67.5 | 155 x 135 x 4.0 |
| D60 | 60 x 60 | - | 100 x 100 x 4.5 |
| D35 | 32 x 24 | - | 50 x 50 x 3-4 |
D60 charts are intended to be used with the Vega light source and are constructed with aluminum, PLA plates, and a magnet mount. .
D35 charts are either between glass plates or mounted in slide frames (glassless).
There are exceptions regarding mounting and size for special charts.

Suitable transparent charts for the following illuminators
| D280 / D240S | D240 | D205 | |
|---|---|---|---|
| Spherical transparency illuminator LE6/LE7 Lightbox illuminator LG3 Sony Pattern Box |
DNP standard viewer | Porta Pattern spherical transparency illuminator |
|
| With adapter | Spherical transparency illuminator LE6/LE7 Lightbox illuminator LG3 |
||
*Chart sizes may vary by +/- 2 mm as they are handmade in house.

