Describing color has always been a complex challenge. Cameras provide their image data in the common sRGB color space, so chances are high that any image you receive without any additional information is represented by the colors in sRGB. Other color spaces, such as those relating to human vision, are used for the analysis of color.
As this analysis is a frequent task, we have created a color cheat sheet, which provides a quick overview of sRGB and CIE-XYZ and the equations for their conversions.
sRGB
The "s" in sRGB stands for "standard" and it is the lowest common denominator in color spaces. It was developed in the 1990s to provide a universal usable color space for display and printers of the time. While there are many different and larger color spaces available, sRGB is still the de facto standard for RGB image data.
CIE-XYZ
CIE (Commission Internationale de l'Éclairage) stands for the International Commission on Illumination, which established color spaces based on colors that can be perceived by the human eye. XYZ does not incorporate negative numbers and instead uses tristimulus values to define the color space that can be seen by the human eye. X represents the linear combination of the cone response non-negative curves created. Y represents luminance and Z is defined as almost equal to blue.
How to Convert
As we are dealing with well-defined color spaces, we can convert from one color space to the other unequivocally. Please see the equations below to help get you started:
sRGB to XYZ
sRGB to sRGB' - Linearize the sRGB Data
sRGB data from a camera, especially when provided in 8bit is normally non-linear, shows the alleged gamma function. We define sRGB as the original camera data with the gamma function applied and sRGB' as the linearized representation.
Please note that we first scale the sRGB data into a range of [0...1], so for 8bit data, we divide all values by 255.
The following calculation is the same for the three channel R, G, and B, which we show with the generically V and V'.
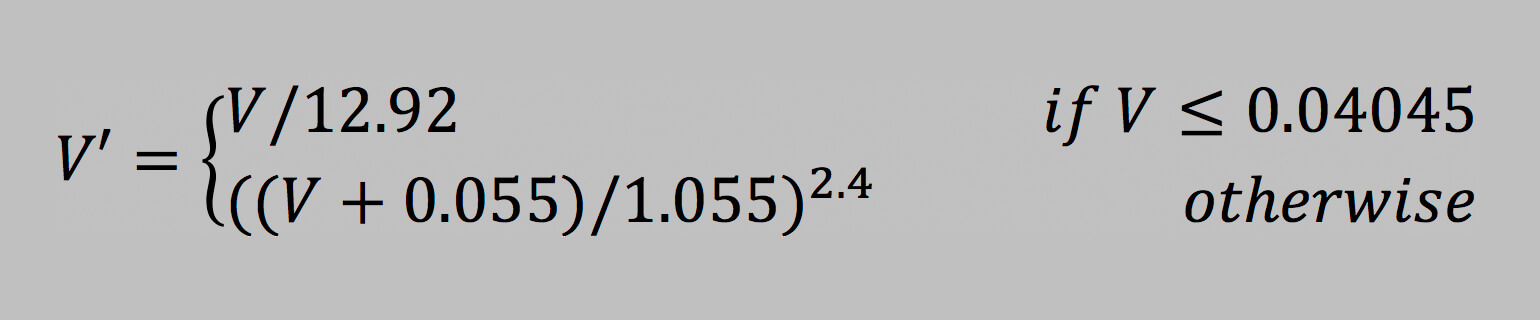
sRGB' to XYZ - apply transformation matrix
A standardized 3x3 matrix describes how to convert from sRGB' data to CIE-XYZ data.

As a quick reminder for those who implement with a tool that does not support matrix calculation easily (e.g. MS-Excel), the calculation of Y as a single equation is here.
![]()
Side note: When we say that Y represents the brightness, we see that green contributes the most and that blue has only a minor effect.
One more Side note: In case you compare your results with the results you get from tools that use an ICC profile (e.g. apply form in Mathworks Matlab) please note: the conversion shown here results into CIE-XYZ data with a reference white point of D65, as defined in the sRGB definition. ICC-Profiles always use D50 as reference white, which you should be aware of when calculating from XYZ to LAB or are comparing to these results.
XYZ to sRGB
To calculate the opposite way, the equations are also straightforward:
XYZ to sRGB' - apply transformation matrix
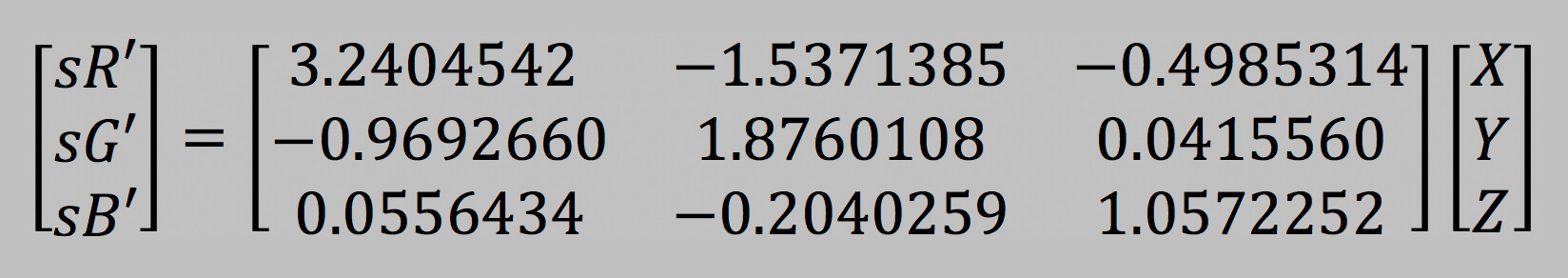
sRGB' to sRGB - apply Gamma

As before, V and V' represent the three channels of sRGB and sRGB' and the equation is applied for each channel.

